Physical constants can take many dimensional forms: dimension refers to the constituent structure of all space (cf. volume) and its position in time; a dimensionless quantity is a quantity without an associated physical dimension. No association to time, length and always has a dimension of 1.
A. Dimensionless ratios:
The fine structure constant α, is the coupling constant characterizing the strength of the electromagnetic interaction (the parameter that describes coupling between light and relativistic electrons and is traditionally associated with quantum electrodynamics) that keeps the atom and the whole universe together. The name comes from the fact that it determines the size of the splitting or fine-structure of the hydrogenic spectral lines. The numerical value of α is the same in all systems of units.
Nobody knows where the alpha number for a coupling comes from, that's why it is 'magic': is it related to pi (as the reduced Plancks constant hbar) or perhaps to the base of natural logarithms? Attempts to find a mathematical basis for this dimensionless constant have continued. It's one of the greatest mysteries of physics: a magic number, we don't know what kind of dance to do on the computer to make this number come out; 29 and 137 being the 10th and 33rd prime numbers. The difference between the 2007 CODATA value for α and this theoretical value is about 3 x 10-11, about 6 * S.E. for the measured value. Today the most accurate value is 137,035999084, the three last unsure. In QED, using the quantum Hall effect or the anomalous magnetic moment of the electron (the "Lande g-factor", g), or with "quantum cyclotron" apparatus.
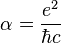
hbar*c = Plancks charge. So it is elemental charge quantized/Plancks charge, or Plancks charge is the ratio of elemental charge and √α? The Planck charge is α^{-1/2} or approx. 11.706 times greater than the elementary charge e carried by an electron.
Stable matter, and therefore life and intelligent beings, could not exist if its value were much different. If alpha were bigger than it really is, we should not be able to distinguish matter from 'ether' (the vacuum, nothingness, grid), (Einstein showed there was no ether). The fact that alpha has just its value 1/137 is certainly no chance but itself a law of nature.
Arnold Sommerfeld introduced the fine-structure constant in 1916.
B. Dimensional ratios: God's units, Unit of measurement, Planck units are physical fundamental units of measurement defined exclusively in terms of five universal physical constants listed below, in such a manner that these five physical constants take the value one when expressed in terms of these units. Planck units elegantly simplify particular algebraic expressions appearing in physical law. Planck units are only one system of natural units among other systems, but are considered unique in that these units are not based on properties of any prototype object, or particle (that would be arbitrarily chosen) but are based only on properties of free space. The constants that Planck units, by definition, normalize to 1 are the:
• Gravitational constant, G;
• Reduced Planck constant, ħ;
• Speed of light in a vacuum, c;
• Coulomb constant, (sometimes ke or k);
• Boltzmann's constant, kB (sometimes k).
Lev Okun in "Trialogue on the number of fundamental constants" Part I "Fundamental constants: parameters and units" 2002:
There are two kinds of fundamental constants of Nature: dimensionless (like α about 1/137) and dimensionful (c — velocity of light, hbar — quantum of action and angular momentum, and G — Newton’s gravitational constant). To clarify the discussion I suggest to refer to the former as fundamental parameters and the latter as fundamental (or basic) units. It is necessary and sufficient to have three basic units in order to reproduce in an experimentally meaningful way the dimensions of all physical quantities. Theoretical equations describing the physical world deal with dimensionless quantities and their solutions depend on dimensionless fundamental parameters. But experiments, from which these theories are extracted and by which they could be tested, involve measurements, i.e. comparisons with standard dimensionful scales. Without standard dimensionful units and hence without certain conventions physics is unthinkable.The third fundamental unit is the fundamental particles.
It is clear that the number of constants or units depends on the theoretical model or framework and hence depends on personal preferences and it changes of course with the evolution of physics. At each stage of this evolution it includes those constants which cannot be expressed in terms of more fundamental, hitherto unknown, ones. At present this number is a few dozens, if one includes neutrino mixing angles. It blows up with the inclusion of hypothetical new particles.
Usually combined with QED, perturbation, but also with gauge and Yukawa couplings in the quantum elemental particle framework with extensions.
Universal fundamental units of Nature.
The number three corresponds to the three basic entities (notions): space, time and matter. It does not depend on the dimensionality of space, being the same in spaces of any dimension. It does not depend on the number and nature of fundamental interactions. For instance, in a world without gravity it still would be three.
The three basic physical dimensions: L, T, M:
Planck 1899 Stoney 1870 [ ]= dimension
l = hbar/mc, l= e√G/c2 velocity [v] = [L/T]
t= hbar/mc2, t= e√G/c3 angular mom. [J] = [MvL] = [ML2/T]
m= hbar*c/G m = e/√G action[S] = [ET] = [Mv2T] = [ML2/T]
Stoney’s (without hbar) and Planck’s units are numerically close to each other, their ratios being √α . Originally proposed in 1899 by Max Planck, these units are also known as natural units because the origin of their definition comes only from properties of nature and not from any human construct. They are generally believed to be both universal in nature and constant in time. Now this picture is challenged.
Gauge couplings.
A coupling constant (g) is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic and interaction part. The coupling constant determines the strength of the interaction part with respect to the kinetic part, or between two sectors of the interaction part (similarity - oscillations?). For example, the electric charge of a particle is a coupling constant, or mass.
If g << 1, it is weakly coupled with perturbation, QED, CKM
If g = /> 1, - it is strongly coupled. An example is the hadronic theory of strong interactions, non-perturbative methods , QCD.
This picture change a bit with the asymptotic degrees of freedom.
The reason this can happen, seemingly violating the conservation of energy, at short times, is the uncertainty relation, result -> quantization in the interaction picture/"virtual" particles going off the mass shell. \Delta E\Delta t >/= hbar This is the Planck scale, where particles vanish 'out of sight' into the virtual Dirac Sea. Gravity is usually ignored (non-renormalisability).
(Toms with asympt. degrees of freedom: If we let g denote a generic coupling constant, then the value of g at energy scale E, the running coupling constant g(E), is determined by E ( dg(E)/dE) = β(E, g) And it can be fused with gravity in Einstein.).
Such processes renormalize the coupling and make it dependent on the energy scale, μ at which one observes the coupling. The dependence of a coupling g (μ) on the energy-scale is known as running of the coupling, and the theory is known as the renormalization group. A beta-function β(g) encodes the running of a coupling parameter, g. If the beta-functions of a quantum field theory vanish, then the theory is scale-invariant. The coupling parameters of a quantum field theory can flow even if the corresponding classical field theory is scale-invariant.
If a beta-function is positive, the corresponding coupling increases with increasing energy. An example is quantum electrodynamics (QED). Particularly at low energies, α ≈ 1/137, whereas at the scale of the Z boson, about 90 GeV, one measures α ≈ 1/127. Moreover, the perturbative beta-function tells us that the coupling continues to increase, and QED becomes strongly coupled at high energy. In fact theoretically the coupling apparently becomes infinite at some finite energy. This phenomenon was first noted by Landau, and is called the Landau pole. Furthermore it was seen that the coupling decreases logarithmically, a phenomenon known as asymptotic freedom, see the Nobel Prize in Physics 2004. This theory was first properly suggested 2006 by Robinson and Wilczek. Confirmed this year by Toms.
David Gross, David Politzer and Frank Wilczek have through their theoretical contributions made it possible to complete the Standard Model of Particle Physics, the model that describes the smallest objects in Nature and how they interact. At the same time it constitutes an important step in the endeavour to provide a unified description of all the forces of Nature, regardless of the spatial scale – from the tiniest distances within the atomic nucleus to the vast distances of the universe.Conversely, the coupling increases with decreasing energy. This means that the coupling becomes large at low energies, and one can no longer rely on perturbation theory. Value is to be used at a scale above the bottom quark mass of about 5 GeV. Each perturbative description depends on a (string) coupling constant. It acts between the quarks, the constituents that build protons, neutrons and the nuclei.
However, in the case of string theory, these coupling constants are not pre-determined, adjustable, or universal parameters; rather they are dynamical scalar fields that can depend on the position in space and time and whose values are determined dynamically.
The Standard Model and the four forces of Nature
You can see how much weaker the other forces coupling constants are from their relative strengths. http://www.physicsmasterclasses.org/downloads/FinalAlphaS_kateshaw.pdf A coupling constant can determine how strong a fundamental force is.
Alpha S is the coupling constant of the strong nuclear force, which is felt between quarks and gluons, g. The Strong Force is the strongest of the four fundamental forces, 1/8.
The weak nuclear force W, Z, for W and Z-bosons, the force between quarks and all leptons, αw is 1/30.
Electromagnetic force depending on photons, felt by quarks and leptons (except neutrinos) are 1/130, and the
gravity depends on the graviton (not found), α G 1/10^39
Unification of forces at 10^19 GeV? GUT scale, the natural scale of quantum gravity in QED (the Planck scale is at 10^35 GeV). At high energies this QED perturbation breaks down. (This GUT scale is seen to maybe not be true. Unification based in part on quantised Yang-Mills (or non-Abelian) gauge fields, is much lower, somewhere near Planck scale, as seen by Toms).
The four forces, from hyperphysics.
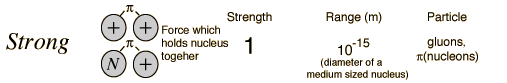
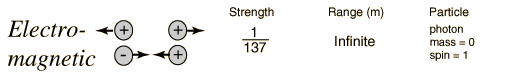
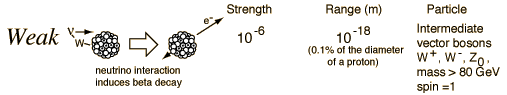
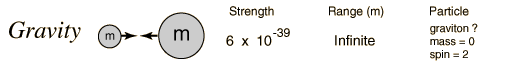
Robinson and Wilczek came up with the idea of gravity-driven asymptotic freedom. Perhaps the most tantalizing effect of QCD and asymptotic freedom is that it opens up the possibility of a unified description of Nature’s forces. When examining the energy dependence of the coupling constants for the electromagnetic, the weak and the strong interaction, it is evident that they almost, but not entirely, meet at one point and have the same value at a very high energy.
Running coupling constants in the Standard Model (left) and with the introduction of supersymmetry (right). In the Standard Model the three lines, which show the inverse value of the coupling constant for the three fundamental forces, do not meet at one point, but with the introduction of supersymmetry, and assuming that the supersymmetric particles are not heavier than about 1 TeV/c2, they do meet at one point. Is this an indication that supersymmetry will be discovered, or a coincidence? (He et.al. showed this relation was not quite true. )
Gravitational constant G: There is no known way of measuring αG directly. Hence αG is known to only four significant digits. Hence the precision of αG depends only on that of G, \hbar and the mass of the electron. A charged elementary particle has approximately one Planck charge, but a mass many orders of magnitude smaller than the Planck unit of mass. The field is much bigger than the particle. The proton is therefore a physical constant. The gravitational attraction among elementary particles, charged or not, can hence be ignored. That gravitation is relevant for macroscopic objects proves that they are electrostatically neutral to a very high degree.
At critical density (the density limit 0 to 4) the matter starts to collapse (into black holes?) as a consequence of the gravitational force, also condensation + energy release happen. Gravity is converted into kinetic energy of mass. This is how we feel weight. In order to condense, energy has to be dissipated from an ever faster rotating cloud and baryonic matter accomplishes this by the electromagnetic effect of emitting photons. Positive pressure needs collisions before it is created because of interaction. Gravity diminishes towards the center of mass, grows outward towards the border/shell. At the center of Earth is no/weak gravity. In universal units or Planck units G is given the value 1. Those photons that travel at the speed of light, c, a velocity that is invariant has a planck unit =1.
Dark matter/antimatter emitts no photons, but do have gravity, seen in gravitational lensings as instance.
We know a lot about the familiar photons, quarks, electrons and other particles that make up ordinary matter because they interact strongly with each other. Scientists can even observe the ghostly neutrino. But there remains the possibility that other particles exist that interact much more weakly. Ideas that explore this hypothesis are called “hidden valley” models, a particle Shangri La that has remained thus far undetected. There are several hidden valley models, including one specific model that incorporates the principle of supersymmetry (MSSM). In this model, a complicated decay signal could reveal signs of a dark photon.There are no dark photons(?) say DZero researchers. They would have explained the
We search for a new light gauge boson, a dark photon. In the model we consider, supersymmetric partners are pair produced and cascade to lightest neutralinos that can decay into the hidden sector state plus either a photon or a dark photon. The dark photon decays through its mixing with a photon into fermion pairs. We therefore investigate a previously unexplored final state that contains a photon, two spatially close leptons, and large missing transverse energy. We do not observe any evidence for dark photons and set a limit on their production.In the case of R-parity conservation (antimatter has R-parity), superpartners are produced in pairs and decay to the SM particles and the lightest superpartner.
Including results from Fermi/LAT, there is evidence of an excess of high energy positrons and no excessive production of anti-protons or photons. The excess can be attributed to the dark matter particles annihilating into pairs of new light gauge bosons, dark photons, which are force carriers in the hidden sector. The dark photon mass can not be much larger than 1 GeV.
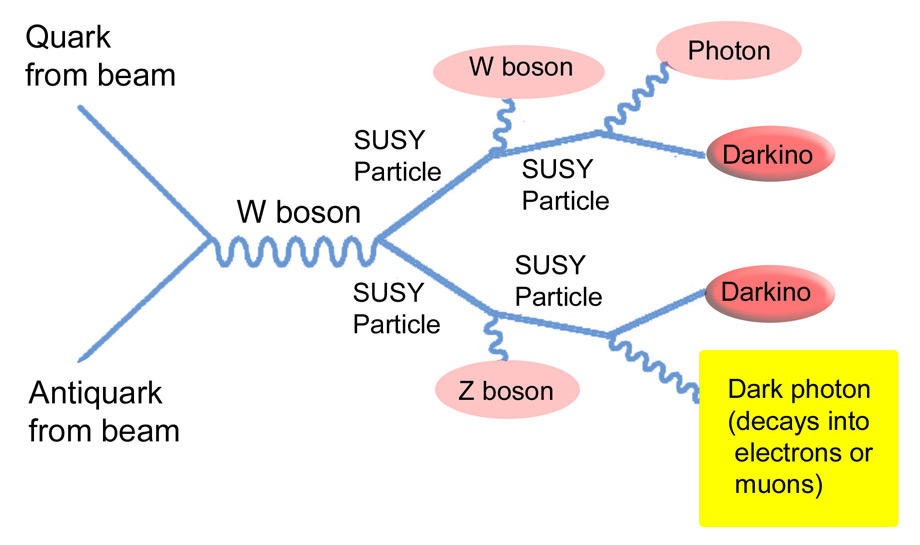In this particular hidden valley model, six particles are created, all indicated by color. The dark photons are shown in yellow. For the other particles, those indicated in light pink will be observed in the detector, while the ones marked with dark pink will escape entirely undetected. If observed, these darkinos might be the dark matter.The Standard Model needs some modification if the dream of the unification of the forces of Nature is to be realised. One possibility is to introduce a new set of particles, and usually supersymmetric particles are thought of, but recent research has shown an asymmetry instead (no clear evidence yet).
Axion oscillating pairs (photonpairs) have been predicted by Wilczek et al.. But they are not found to be part of the dark matter.
From the Nobel lecture: "The Standard Model also needs modification to incorporate the recently discovered properties of neutrinos - that they have a mass different from zero. In addition, perhaps this will lead to an explanation of a number of other cosmological enigmas such as the dark matter that seems to dominate space."
This is what Kea does.
Asymptotic degrees of freedom.
"The fantastic and unexpected discovery of asymptotic freedom in QCD has profoundly changed our understanding of the ways in which the basic forces of Nature in our world work, says Wilczek et al.. Toms 2010:
However, it is possible instead to view Einstein gravity as an effective theory that is only valid below some high energy scale. The cut-off scale is usually associated with the Planck scale, EP approx. 10^19GeV, the natural quantum scale for gravity. Above this energy scale some theory of gravity other than Einstein’s theory applies (string theory for example); below this energy scale we can deal with quantised Einstein gravity and obtain reliable predictions. Adopting this effective field theory viewpoint it is perfectly reasonable to include Einstein gravity with the standard model of particle physics and to examine its possible consequences using quantum
field theory methods. Quantum gravity leads to a correction to the renormalisation group β-function (not present in the absence of gravity) that tends to result in asymptotic freedom; this holds even for theories (like quantum electrodynamics) that are not asymptotically free when gravity is neglected.
The value of the “running” coupling constant as, as a function of the energy scale E. The curve that slopes downwards (negative beta function) is a prediction of the asymptomatic freedom in QCD.
According to their theories, the force carriers = gluons have a unique and highly unexpected property, namely that they interact not only with quarks but also with each other. This property means that the closer quarks come to each other, the weaker the quark colour charge and the weaker the interaction. Quarks come closer to each other when the energy increases, so the interaction strength decreases with energy. This property, called asymptotic freedom, means that the beta function is negative. On the other hand, the interaction strength increases with increasing distance, which means that a quark cannot be removed from an atomic nucleus. The theory confirmed the experiments: quarks are confined, in groups of three, inside the proton and the neutron but can be visualized as “grains” in suitable experiments.
Asymptotic freedom makes it possible to calculate the small distance interaction for quarks and gluons, assuming that they are free particles. By colliding the particles at very high energies it is possible to bring them close enough together.
Unification at Planck scale, Planck constant?
Two reports coherently describes the unification all the way up to energies below the Planck scale. First Toms in Nature and He et al. in arXive. They demonstrate that the graviton-induced universal power-law runnings always assist the three SM gauge forces to reach unification around the Planck scale, irrespective of the detail of logarithmic corrections. With implementions for the Higgs boson mass. "We are interested in all the bilinear terms of background photon field, which correspond to the one-loop self-energy diagrams."
Graviton induced radiative corrections for photon self-energy: the wavy external (internal) lines stand for background (fluctuating) photon fields, the double-lines for gravitons, the dotted lines for photon-ghosts, and the circle-dotted line for graviton ghosts. He et al.
More precise numerical analyses including two-loop RG running reveal that even in MSSM the strong gauge coupling α3 does not exactly meet with the other two at the GUT scale as its value is smaller than (α1, α2) by about 3%. With the gauge-invariant gravitational power-law corrections, we can resolve running gauge coupling αi(μ) = gi^2 (μ)/4π, they say. Hence, the universal gravitational power-law corrections will always drive all gauge couplings to rapidly converge to the UV fixed point at high scales and reach unification around the Planck scale, irrespective of the detail of their logarithmic corrections and initial values. It is useful to note that there are clear evidences supportingToms 2008: Quantum gravity is shown to lead to a contribution to the running charge not present when the cosmological constant vanishes. We show the possibility of an ultraviolet fixed point that is linked directly to the cosmological constant.
Einstein gravity to be asymptotically safe via the existence of nontrivial UV fixed point in its RG flow, so it may be UV complete and perturbatively sensible even beyond the Planck scale.
The speed of light c has already been implicitly used in order to talk about the area of a surface embedded in space-time. This fact allows us to replace hbar by a well defined length, λs, which turns out to be fundamental both in an intuitive sense and in the sense of S. Weinberg. Indeed, we should be able, in principle, to compute any observable in terms of c and λs. String theory (OST) only needs two fundamental dimensionful constants c and λs, i.e. one fundamental unit of speed and one of length.
The apparent puzzle is clear: where has our loved hbar disappeared? My answer was
then (and still is): it changed its dress! Having adopted new units of energy (energy being replaced by energy divided by tension, i.e. by length), the units of action (hence of hbar) have also changed. And indeed the most amazing outcome of this reasoning is that the new Planck constant, λs^2 is the UV cutoff.
He et.al. also shows that
...for the SM gauge coupling evolutions, despite their familiar non-convergence in the region of 10^13−17 GeV, the three couplings do unify around the Planck scale. For the MSSM, one needs not to worry about the model-dependent threshold effects or the two-loop-induced non-convergence around the scale of 10^16 GeV, it is quite possible that the GUT does not happen around the scale of 10^16 GeV, as in the SM case. Instead, the real GUT would be naturally realized around the Planck scale, and thus is expected to simultaneously unify with the gravity force as well. This also removes the old puzzle on why the conventional GUT scale is about three orders of magnitude lower than the fundamental Planck scale. Furthermore, the Planck scale unification helps to sufficiently postpone nucleon decays, which explains why all the experimental data so far support the proton stability. In addition, this is also a good news for various approaches of dynamical electroweak symmetry breaking, such as the technicolor type of theories...
Extrapolation of experimental values, measured at relatively large distances (not shown), for the strength of the strong force (αS), weak force (αW) and hypercharge force (αY) indicates that these forces might merge with gravity for processes characterized by distance scales that are at least 13 orders of magnitude smaller than those currently being explored with the Large Hadron Collider (LHC). The strength of gravity is characterized by αG, and the strength of the electromagnetic force is not shown because at the distance scales displayed this force is replaced by the combination of the weak and hypercharge forces. Toms's analysis investigates a piece of the puzzle that theorists must resolve to correctly describe this unification: the behaviour of gravity in the range between 10−32 and 10−35 metres.S. Robinson and F. Wilczek, Phys. Rev. Lett. 96, 231601 (2006) [arXiv:hep-th/0509050].
To be continued.
Inga kommentarer:
Skicka en kommentar