Atomic periodic table of shapes.

"We're trying to build a periodic table of shapes," says Tom Coates, a mathematician at Imperial College London.

Video at NS: Atoms in periodic table of shapes

A new dimension for mathematics – the Periodic Table of shapes
Mathematicians are creating their own version of the periodic table that will provide a vast directory of all the possible shapes in the universe across three, four and five dimensions, linking shapes together in the same way as the periodic table links groups of chemical elements. The three-year project, announced today, should provide a resource that mathematicians, physicists and other scientists can use for calculations and research in a range of areas, including computer vision, number theory, and theoretical physics. For some mental exercise, check out these animations ,2, 3, that have already been analyzed in the project.

"Most people are familiar with the idea of three-dimensional shapes, but for those who don't work in our field, it might be hard to get your head around the idea of shapes in four and five dimensions. However, understanding these kinds of shapes is really important for lots of aspects of science. If you are working in robotics, you might need to work out the equation for a five dimensional shape in order to figure out how to instruct a robot to look at an object and then move its arm to pick that object up. If you are a physicist, you might need to analyse the shapes of hidden dimensions in the universe in order to understand how sub-atomic particles work. We think the work that we're doing in our new project will ultimately help our colleagues in many different branches of science. In our project we are looking for the basic building blocks of shapes. You can think of these basic building blocks as 'atoms', and think of larger shapes as 'molecules.' The next challenge is to understand how properties of the larger shapes depend on the 'atoms' that they are made from. In other words, we want to build a theory of chemistry for shapes," added Dr Coates.

We are searching for special shapes, called Fano varieties, that are the “elements” in our “periodic table of shapes”. We created the images above when analyzing 3-dimensional Fano varieties. It is difficult to visualize a complex 3-dimensional shape, but one way to do it is to look at slices through the shape. For example, to visualize the human brain (which is also a complex 3-dimensional shape!) you can take slices using an MRI scanner, and then assemble these slices to view the whole brain, like this: (Thanks to Dr Daniel Bulte at the University of Oxford for the animation.)

Note: Abelian/non-abelian correspondence is similar for pairs 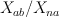and 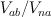. Mirror symmetry.

Dr Coates has recently won a prestigious Philip Leverhulme Prize worth GBP70,000 from the Leverhulme Trust.

To follow the research project in real time, visit his blog.
Links to superconductivity.