Living matter is different from non-living in a number of ways:
1. Open entropic systems, that means the mass is relative and changeable. Form and structure as topology, fractality and hierarchy are relatively stable? Superconduction and solitons are used?
2. Negentropy is selected for, in terms of information. What exactly describes that information? Patterns, densities, but also meanings, new creation of patterns that are pure mathemathical? Negentropy is conserved and renewed or recombined, conserved in DNA and memory (as a chrystal phase?), recombined in mutations, learnings and adaption.
3. Complexity and networkings, signalling near and far away. See pt. 5.
4. Self-organization, healing and regeneration, differentation.
5. Growing, regeneration of a self, selfreplication as new individuals (reproduction), propagation, , spreading of the negentropy.
6. Adaption, change, mutation.
Negentropy is in the zero point? Quantum world? The Dirac Sea, QCD vacuum? Life is quantal?
If I was God I would certainly look very close on this A-phase of matter to see if it could be used to create Life, forms and structures?
Sanda: "I do not think that all these conditions have been chosen randomly. I suspect that the Mother Nature has gone out of Her way to show us CP violation, and She is also showing us the way to the fundamental theory." in The Road to the Discovery of Large CP Violation in B Decays. A Miracle Story.

Three ways to look.
1. From our wiev: The models of Universe can either begin with the electronuclear force symmetry as fundamental property that then will be broken (GUT, with no gravity, top-bottom) Or as a reductionistic wiev with ever smaller parts from the bigger ones (a deeper understanding is gained by dividing things into smaller parts)
2. From Big Bang wiev: with anti-GUT where symmetry is gradually built in and created (bottom-up) An emergent wiev (particle-wave duality -> origin of particles = origin of waves).
Superstring theory as opposed to condensed matter theory, acc. to Wen. Different organizations (orders, phases) of particles leads to different kinds of waves and wave equations. Different organizations -> different waves -> different kinds of particles.
Originate from organization = principle of emergence.
3. The holistic approach is the third way. Holism= can be seen in every part too. Creation. Environment is important. Holism is the fundamental union? This is the Creators wiev?
I think this is important to keep in mind.
First some basics.
CP symmetry (charge conjugation and parity symmetry) states that the laws of physics should be the same if a particle were interchanged with its antiparticle and left and right were swapped (incl. time). The strong interaction and electromagnetic interaction seem to be invariant together under the combined CP transformation operation, but not during certain types of weak decay. Weak interactions violate the P symmetry or, as the analogy goes, some reactions did not occur as often as their mirror image. Asymmetry is born.
Addition: Parity is also violated now by strong interaction (Taylor Muzzin)? The physicist is still quick to point out that the effect only suggests parity violation - it doesn't prove it. If the effect proves to be real, it could help scientists understand a similar asymmetry that led to one of physics' most fundamental mysteries - namely, why the universe is dominated by ordinary matter today.
Parity was long thought to be a fundamental law of nature. It essentially states that the universe is neither right- nor left-handed — that the laws of physics remain unchanged when expressed in inverted coordinates. In the early 1950s it was found that the so-called weak force, which is responsible for nuclear radioactivity, breaks the parity law. However, the strong force, which holds together subatomic particles, was thought to adhere to the law of parity, at least under normal circumstances. Now this law appears to have been broken by a team of about a dozen particle physicists, including Jack Sandweiss, Yale’s Donner Professor of Physics. Since 2000, Sandweiss has been smashing the nuclei of gold atoms together as part of the STAR experiment at RHIC. The plasma “bubble” created in the collisions at RHIC lasted for a mere millionth of a billionth of a billionth of a second, yet the team hopes to use it to learn more about how structure in the universe — from black holes to galaxies — may have formed out of the soup. Parity violation is very difficult to detect, but the magnetic field in conjunction with parity violation gave rise to a secondary effect that we could detect.
And in Physical Review Letters/RHIC/Science Daily, II, Physicists have predicted an increasing probability of finding such bubbles, or local regions, of "broken" symmetry at extreme temperatures near transitions from one phase of matter to another. According to the predictions, the matter inside these bubbles would exhibit different symmetries - or behavior under certain simple transformations of space, time, and particle types - than the surrounding matter.
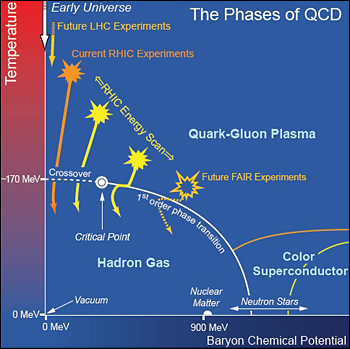 Schematic QCD phase diagram for nuclear matter. The solid lines show the phase boundaries for the indicated phases. The solid circle depicts the critical point. Possible trajectories for systems created in the QGP phase at different accelerator facilities are also shown.
Schematic QCD phase diagram for nuclear matter. The solid lines show the phase boundaries for the indicated phases. The solid circle depicts the critical point. Possible trajectories for systems created in the QGP phase at different accelerator facilities are also shown.The CP violation (Nobel prize 1980, 2008) discovery once shocked particle physics and opened up questions still at the core of particle physics and cosmology. The lack of an exact CP symmetry, but also the fact that it is so nearly a symmetry, created a great puzzle. A weaker variant, the CPT symmetry (T=time, reversal of motion in time) came up, but a violation of the CP symmetry is equivalent to a violation of the T symmetry.
There are also other symmetries. Geometric symmetries, permutation symmetries, space-time symmetries, gauge symmetries... R-symmetry, dynamical symmetries based on vibrational and rotational symmetries etc. Algebraic and other mathematical structures are at the basement.
To create the required imbalance in matter and antimatter, because our Universe is made of matter, (asymmetry, chirality, no antimatter) out of an initial condition of balance, the Sakharov conditions must be satisfied, one of which is the existence of CP violation during the extreme conditions of the first seconds after the Big Bang (the violation of CP symmetry is a necessary condition for baryogenesis, the process thought to be responsible for the matter-antimatter asymmetry of the universe.) Also creation of magnetic monopoles did happen then? The laws of physics distinguish between matter and antimatter.
The Big Bang should have produced equal amounts of matter and antimatter if CP symmetry was preserved with total cancellation (annihilation) of both- protons should have cancelled with antiprotons, electrons with antielectrons, neutrons with antineutrons, and so on for all elementary particles. This would have resulted in a sea of radiation in the universe with no matter. Since this is not the case, after the Big Bang, physical laws must have acted differently for matter and antimatter, i.e. violating CP symmetry. - The 4% difference is fundamental in the chirality? (TGD-diary, A new dark matter anomaly, 1.10, 2009.). Today this is debated in the neutrino- antineutrino oscillation results.
Explanations which do not involve CP violation are less plausible, since they rely on the assumption that the matter–antimatter imbalance was present (implicitly?) at the beginning, or on other admittedly exotic assumptions.
The other Sakharov conditions were the stability of proton (baryon) and that the cosmos originated in the heat of the Big Bang (equilibrium violated).
So we get a polarity here between the symmetry and the stability and the product is matter.
The true ground state of the quarks is quite different from the naive fermi balls. It is characterized by the formation of a coherent condensate, and the development of an energy gap. The condensation, which is energetically favorable, is inconsistent with a magnetic field, and so weak magnetic fields are expelled. This is the famous Meissner effect in superconductivity, which is essentially identical to what is known as the Higgs phenomenon in particle physics. Wilchek 1999.
Quantum Field Theory, reductionistic wiev, explains nature's electromagnetic, weak and strong nuclear forces (though not gravity). The boson/fermion dichotomy is mandated by the Spin-Statistics Theorem of QFT. Elementary particles are classified into bosons and fermions (anyons, are neither). The distinction is made on the basis of the symmetry of their wavefunction upon particle exchange. As the identical particles are indistinguishable, exchange of two particles changes the wavefunction at most by a factor C. The choice of the sign of C is intimately linked to the spin quantum number of the particles, namely, particles having an integer spin quantum number take C = +1 and are called bosons, whereas those with a half-odd spin take C = −1 and are called fermions. Doing the two-particle exchange twice brings the system back to the original situation, so that C2 = 1, and hence C = ±1.
Bosons can pile on top of one another without limit (superposition), all occupying the same quantum state. Why? The phi-state? The infinities, polarities? At low temperatures (low entropy), this causes phenomena as superconductivity, superfluidity and Bose-Einstein condensation. It also allows photons of the same frequency to form coherent laser beams.
Fermions, on the other hand, avoid one another. Electrons around a nucleus stack into shells (octonions) instead of collapsing into a condensed cloud, giving rise to atoms with a great range of chemical properties. Thus the nucleus determine the electron charachter. Unity is bosonic, differentiation is fermionic.
Bosons, which are governed by Bose-Einstein statistics, are particles/waves with an intrinsic integer spin of 0, 1, 2 or other integer, and include photons, W and Z bosons, and gluons. They are often force carrier particles. Bosons may be either elementary, like photons, or composite, like mesons, some are not truly bosons (e.g. helium-4 atoms); a more accurate term for such composite particles would be "bosonic-composites", and are important in superfluidity and other applications of Bose–Einstein condensates. A composite particle containing an even number of fermions is a boson, since it has integer spin. As instance, the nucleus of a carbon-12 atom contains 6 protons and 6 neutrons (all fermions) and is therefore a boson; The spin is the important thing.
- Photons are the force carriers of the electromagnetic field.
- W and Z bosons are the force carriers which mediate the weak nuclear force (seen 1983) can get mass; the charged vector boson W+/- carries a superposition of weak and electromagnetic charges, whereas the neutral vector boson Z0 carries only the weak isospin charge. The W boson can have a positive or negative charge (+1 or -1), and the Z boson is electrically neutral. Z bosons can only transfer momentum, and their interactions are therefore called neutral current interactions..
- Gluons are the fundamental force carriers underlying the strong nuclear force, and they have a spin of +1. There are eight distinct gluons (colors), each their own antiparticle. No free state gluons have been observed.
- X and Y bosons may or may not exist, it is presumed that they would allow for a new force which would bind particles called leptons (as electrons) to particles called quarks (as protons).
- All particles have a sort of angular momentum which is labeled spin. This spin gives the magnetic properties. Some say the Higgs particle is spinless (an anyon?). Charges are often called the coupling constants because their strength determines the coupling, or interaction strength with the corresponding fields.
The standard model postulates the existence of Higgs bosons, which give other particles their mass via the Higgs mechanism. After symmetry breaking, three of the four degrees of freedom in the Higgs field mix with the W and Z bosons (naturally massless), that get mass, while the one remaining degree of freedom becomes the Higgs boson – a new scalar particle, and its own antiparticle (a quasiparticle?). Other numbers of possible Higgs bosons are also calculated, and other Higgs mechanisms. In QCD, condensed matter physics, it is the gluon that get mass. So the options is between the weak and the strong forces. Notice there are no virtual charges without virtual mass.
Fermions, governed by Fermi-Dirac statistics, are all particles with odd-half-integer spins – ½, 3/2, 5/2, etc. – and include the electron, neutrinos, muons and all the quarks = the fundamental particles that make up protons and neutrons. Fermions are usually associated with matter, although Majorana and massless Weylfermions is also. Only one fermion can occupy a quantum state at a given time (Pauli exclusion princip). This results in "rigidity" or "stiffness" of states (atomic nuclei, shells, atoms, molecules, etc.).
There are two types of elementary fermions: quarks and leptons. In total, there are 24 different fermions: being 6 quarks and 6 leptons, each with a corresponding antiparticle:Life is very much bosonic. But Life doesn't act in low temperatures to eliminate the entropy because Life needs re-actions. Instead Life creates negentropy, or select it from the bosonic world. Coherence? Negentropic oscillations? Life is creative, interacting.
- 12 quarks - 6 particles (u · d · s · c · b · t) with 6 corresponding antiparticles (u · d · s · c · b · t)
Composite fermions, such as protons and neutrons (hadrons) are essential building blocks of matter. Weakly interacting fermions can also display bosonic behaviour, as in superconductivity. The known fermions of left-handed helicity experience weak interactions while the known right-handed fermions do not. Or put another way, only left-handed fermions and right-handed antifermions interact with the W boson.
- 12 leptons - 6 particles (e− · μ− · τ− · νe · νμ · ντ) with 6 corresponding antiparticles (e+ · μ+ · τ+ · νe · νμ · ντ)
Interactions.
Bosons never become fermions?
Composite particles: Electrons having spin ½ are fermions. In our three-dimensional(3D) world, the distinction between fermions and bosons is strictly enforced. In a two-dimensional (2D) world, however, the rule can be relaxed by a trick called flux attachment. One can transform a fermion to a boson (or vice versa) by attaching to it fictitious magnetic flux(es), which takes care of the change in the phase of its wavefunction. No transformation of the exchange path is possible in 2-D, but in 3-d, yes. In surfaces, not spheres.
Elementary particles: Bosons play by one set of rules while fermions, including electrons, play by another. Do bosons ever play by fermion rules? Specifically, do photons act like bosons all the time, or could they sometimes act like fermions? The answer is a solid "no."
So, there can be no bosonic 'emergence' into matter at particle level. Bosons can never be massive particles (only W- and Z bosons slightly)? Like photons they can only interact by giving energy as a power of time (light speed). They are gauge bosons. Energy is bosonic? The energy content is not dependent on matter either. At the end everything is energy. Everything is controlled by forces, but emergent quantal properties is made manifest only through composite bosons.
Matter is no 'condensation' of energy? Matter is a relaxation of energy from a superpositional quantal bosonic state, coming from the CP(T)-violation? Like a phase shift. And Life has very much more narrow constrictions than ordinary matter. Like a phase in a phase.
The electric force depends only on charge (bosonic; in fields=mediators) and not on the particular nature of particles. For example, the electric force between two muons, which are particles with the same charge as the electron but 200 times heavier, is equal to that between two electrons in the same external conditions. Since our physical world has 3-D, electric and magnetic fields are 3-component vectors defined at every point in space. Equivalently, the fields are vector-valued functions of space. A point-like particle with positive (negative) electric charge has an electric field radially pointing outwards (inwards). Electric charges are also responders to the electric field, but neutrons have no field (neutral) and no respons.Electrons can also be fractionalized and still have the same charge? What about ions then? The ion theory is not true? The ion is magnetic mostly? What is the electricity? Like photons it can travel, it is invisible, it responds to other charges. The mass can vary, but the charachter is the same. The time factor is excluded in this reasoning. Time is important too. What is time? Travelling and motions are time.
The fractional quantum Hall effect (FQHE) is a physical phenomenon in which a certain system behaves as if it were composed of particles with charge smaller than the elementary charge. Seen 1982, Nobel prize 1998. The effect is a manifestation of simple collective behaviour in a 2-D system of strongly interacting electrons. At particular magnetic fields, the electron gas condenses into a remarkable state with liquid-like properties. The electron can get bosonic properties in certain conditions. Is the electron a true fermion?
Electrons can be composite and chiral? What do that? Vortices?
An electron accompanied by an odd number of fluxes can be regarded as a composite boson. Therefore, the ν = 1 and ν = 1/3 QHE states can be viewed as a composite boson gas in zero magnetic field, and the QHE states can be interpreted as superfluid states of those composite bosons.
It is the magnetism that keeps the electron as a particle. The nucleus decide? The parity? An open parity (broken symmetry) gives a different spin and an ion? Broken symmetries are energetically instabile in that context.
The fundamental building blocks of the fractional quantum Hall effect are also composite fermions, which are electrons with an even number of quantized vortices attached to them. An even number flux quanta are captured by each electron, forming integer-charged quasiparticles. This makes electrons at a filling factor 1/3, for example, behave in the same way as at filling factor 1. A remarkable result is that the filling factor 1/2 corresponds to zero magnetic field for composite fermions, resulting in their Fermi sea.
Fractionally charged quasiparticles are neither bosons nor fermions and exhibit anyonic statistics. The fractional quantum Hall effect continues to be influential in theories about topological order.
Strong force - nuclear force - electric and magnetic dipole - gravity.
But neutrons bear the strong gluon force, 100 times the EM-force, and a 'field of gauge bosons'= gluon field, but are neutral? This force is not electric and weak, not gravitional. It is 'color' in the quarks. It is magnetic but without electricity. An anomalous magnetism? In the nucleus they are stable but not as free nucleons or neutronium, that's why they determine the isotopes and go through beta-decay. The only possible decay mode without a change of baryon number is for one of the quarks to change flavour via the weak interaction. The neutron consists of two down quarks with charge −1⁄3 e and one up quark with charge +2⁄3 e, and the decay of one of the down quarks into a lighter up quark can be achieved by the emission of a W boson. By this means the neutron decays into a proton (which contains one down and two up quarks), an electron, and an electron antineutrino. Inside a nucleus, protons can also transform into a neutron via inverse beta decay. This transformation occurs by emission of a antielectron (also called positron) and a neutrino. The small and inhomogenous magnetic moment is an indication of substructure, i.e. that the neutron is made of other, electrically charged quarks.
 Diagram of a strong proton-neutron interaction with the individual quark constituents shown, to illustrate how the fundamental strong interaction gives rise to the nuclear force. Straight lines are quarks, while multi-colored loops are gluons (the carriers of the fundamental force). Time proceeds from left to right. A neutral pion in middle. Wikipedia.
Diagram of a strong proton-neutron interaction with the individual quark constituents shown, to illustrate how the fundamental strong interaction gives rise to the nuclear force. Straight lines are quarks, while multi-colored loops are gluons (the carriers of the fundamental force). Time proceeds from left to right. A neutral pion in middle. Wikipedia. Decay is balanced against the instability of repulsive protons in bound states in nuclei. Also protons, which are stable in empty space, may transform into neutrons when bound inside of a nucleus. More neutrons are required in atoms with large numbers of protons.
Interaction through gravity, weak force. The neutron is an electric dipole with a magnetic moment and no net electricity. A tiny separation of positive and negative charge within the neutron leading to a permanent electric dipole moment.
Nuclear force:
Since nucleons have no color charge, the nuclear force does not directly involve the force carriers of quantum chromodynamics, the gluons. However, just as electrically neutral atoms (each composed of cancelling charges) attract each other via the second-order effects of electrical polarization, via the van der Waals forces (London forces), so by analogy, "color-neutral" nucleons may attract each other by a type of polarization which allows some basically gluon-mediated effects to be carried from one color-neutral nucleon to another, via the virtual mesons which transmit the forces, and which themselves are held together by virtual gluons. It is this van der Waals-like nature which is responsible for the term "residual" in the term "residual strong force."No wonder physicians avoid bond states, but Life is about complexity. How could these immense degrees of freedom be fixed? Only through entanglement (bosonic state) into bigger bits, qubits. These are made topologically in a fractal way. If I was God I would try that way.
Such systems can be described by attributing a potential (such as the Yukawa potential) to the nucleons and using the potentials in a Schrödinger equation. The form of the potential is derived phenomenologically. Nuclear interactions from the basic interactions in many-body systems are difficult to calculate. In particular, chiral symmetry breaking can be analysed in terms of an effective field theory (called chiral perturbation theory) which allows perturbative calculations of the interactions between nucleons with pions as exchange particles. The pion decay constant may be viewed as a measure of the magnitude of the chiral symmetry breaking.
W-boson electric dipole... known leptons and quarks are not elemental but topological condensates. Heavy leptons and quarks are excited states with spin 1/2, 3/2 etc. with the same quantum numbers as the existing fermions. Interactions between ordinary and heavy fermions tend to be of magnetic type, mediated by gauge bosons. The chirality means that the interaction is only to lefthanded, and the interaction with electrons are about 0,5 when one handedness is left out.
Photons (gives electromagnetism) without mass travel with the same velocity in spite of different energylevels. As do nerve pulses. Mass-independence. And thence also gravity-independence? See the Michelson-Morley experiment. Gravity's main aspect is attraction, and it is felt and influenced by all energy, everywhere. Even light loses energy in the gravitational field of a massive body, as in black holes. The graviton is thought to be responsible for gravity, or gravity is emergent through mass. Magnetism can generate gravity, says Jerry Decker. How? We look at that later. It would be natural if gravity would be emergent, when it has no room in QFT.
Can fermions act as bosons?
Only as composites. But this matter as wave-function? What is it then? Neutral (iniert) particles and fields - and gravity? The interaction happens at the bosonic composite level? In 2-D but not in 3-D? The complexity has always been seen as an obstacle. Gravity is a surface-entanglement problem?
Complexity - relaxation in bound states. And 'emergence' of new dimensions? A topological paradigm?
If I was God and tried this puzzle, I would try to lay one piece upon the other and make them fuse. Then I needed only the basic degrees of freedom? It would be much more simple? Bosonic states of matter would be interesting. Like carbon. Maybe I could use carbon?
Fermionic or bosonic behavior of a composite particle/system is only seen at large (compared to size of the system) distance. At proximity, where spatial structure begins to be important, a composite particle (or system) behaves according to its constituent makeup. Fermions can exhibit bosonic behavior when they become loosely bound in pairs, as quasiparticles. This is the origin of superconductivity and the superfluidity of helium-3: in superconducting materials, electrons interact through the exchange of phonons, forming Cooper pairs, while in helium-3 (fermion), Cooper pairs are formed via spin fluctuations (paramagnetism).
Fractionally-charged quasiparticles based on accurate trial wave functions for the ground state at fraction 1 / q as well as its quasiparticle and quasihole excitations. The excitations have fractional charge. The FQH effect shows the limits of Landau's symmetry breaking theory. Previously it was long believed that the symmetry breaking theory could explain all the important concepts and essential properties of all forms of matter. Different FQH states all have the same symmetry and cannot be described by symmetry breaking theory. Thus FQH states represent new states of matter that contain a completely new kind of order—topological order. FQH liquids indicates that there is a whole new world beyond the paradigm of symmetry breaking, a basic topological paradigm, greatly enrich our understanding of quantum phases and quantum phase transitions. The associated fractional charge, fractional statistics, non-Abelian statistics, chiral edge states, etc demonstrate the power and the fascination of emergence in many-body systems.
This fractional charge tells also about hierarchy? The hierarchy of quantum Hall states is associated with a corresponding hierarchy of classical fluids. Results are given for the energy at many rational filling factors and for the pair-correlation function at ν=2/7. There can be field configurations of bosons which are topologically twisted. These are coherent states (or solitons) which behave like a particle, and they can be fermionic even if all the elementary particles are bosons. Fermions made of bosons are named Skyrmions, and involves fields which take values on a 3-D sphere. In Skyrme's model, which is reproduced in the large N or string approximation to QCD, the proton and neutron are fermionic topological solitons of the pion field. In the chiral limit when the light quark masses mu,md,ms tend to zero, such that the octet of the pseudoscalar mesons π,K, η become nearly massless (pseudo) Goldstone bosons, they are the lightest degrees of freedom of QCD. The other three quark masses are heavy, tend to infinity.
- One very light, almost nothing, one very heavy? Like a quasiparticle?
The model is not good in small N. If the mean field happens to be small, the valence level is shallow, the Dirac sea is weakly distorted, and there are few antiquarks. In this case the model reproduces the well-known spin and space quark wave functions of the nonrelativistic models for baryons. If, on the contrary, the mean field happens to be very broad, the valence level dives towards the negative-energy Dirac sea, and there are O(Nc) (that is many!) additional Q¯Q pairs in a baryon, whose energy can be approximated by the two- and four-derivative Skyrme Lagrangian. The realistic picture is somewhere in between the two extremes.
Understanding the quark origin it becomes possible to formulate what is the Skyrmion in terms of quarks and demystify the famous prescription of the Skyrme model that a chiral soliton with a topological (or winding) number equal to unity, is in fact a fermion.The Skyrmion is nothing but the mean chiral field binding quarks in a baryon.
CKM-matrix, Kobayashi and Maskawa’s calculation matrix, contains probabilities for describing how the transformation of the quarks will take place. Found the solution in a 3 x 3 matrix in flavour-changing weak decays, as instance, the object that couples to the up quark via charged-current weak interaction is a superposition of down-type quarks. A rotational matrix is used. It turned out that the quarks and antiquarks swapped identity with each other within their own family. Quasiparticles - soliton? If this exchange of identity with double broken symmetry was to take place between matter and antimatter, a further quark family was needed in addition to the other two. Three is needed to get a CP-violation. Small hints is at a fourth generation too?
On the left is the weak interaction doublet partners of up-type quarks, and on the right is the CKM Matrix along with a vector of mass eigenstates of down-type quarks. The CKM matrix describes the probability of a transition from one quark i to another quark j. These transitions are proportional to |Vij|2.
The sum of all couplings of any of the up-type quarks to all the down-type quarks is the same for all generations. This relation is called weak universality. A rotational, mixing angle θc, now called the Cabibbo angle, between the d and s quarks resolve the second level. For the Standard Model case (N = 3), there are three mixing angles and one CP-violating complex phase. This requires a top quark?For any fixed and different i and j, this is a constraint on three complex numbers, one for each k, which says that these numbers form the sides of a triangle in the complex plane. There are six choices of i and j (three independent), and hence six such triangles, each of which is called an unitary triangle. Their shapes can be very different, but they all have the same area, which can be related to the CP violating phase. The area vanishes for the specific parameters in the Standard Model for which there would be no CP violation. The orientation of the triangles depend on the phases of the quark fields. The total number of free variables independent of the choice of the phases of basis vectors is N2 − (2N − 1) = (N − 1)2. The masses and mixings of quarks have a common origin from the Yukawa interactions (potentials) with the Higgs condensate in SM. There are many possible parameterizations. The neutrino Koide triplet is the newest?

Sketch of the unitarity triangle. The six vanishing combinations can be represented as triangles in a complex plane, of which the ones obtained by taking scalar products of neighboring rows or columns are nearly degenerate.
Note: Some sort of deep physical asymmetry between up-type and down-type quarks maybe are, and thus CKM is not totally unitary. A small difference between inverse and conjugate transpose is possible. The first evidence is here for an anomalous CP violation in the mixing of neutral B mesons.
It should be possible to study a major violation of symmetry in B-meson particles, which are ten times heavier than their cousins, the kaons. Among other, the BaBar particle detectors is doing that. The first generation of CP violation experiments in the B-system, Belle and Babar at the B-factories, constrain the CKM matrix already considerably. The search for new physics beyond the Standard Model requires much larger statistics, combined with the study of other B-meson decays than those accessible at the B-factories. The aim is to exploit the copious production of all B-flavours at the LHC: ATLAS, CMS and LHCb.
While Skyrme's example involves pion physics, there is a much more familiar example in QED with a magnetic monopole. A bosonic monopole with the smallest possible magnetic charge and a bosonic version of the electron would form a fermionic dyon.
This is something geometric? Angles, form, structure? To me this resembles the code matrix in the genetic code. Also there are 24 'letters' (as the number of fermions). A code of materialization? Complex numbers consisting of a real and imaginary part and used in cubic equations containing the square roots of negative numbers, the theory of quaternions, complex Lie algebra, etc . A scale parameter is also present. Marni writes: It is not yet clear why conjugation on the should correspond to antineutrinos, but recall that conjugation is a standard feature of phases for antiparticles in the braid spectrum. The component appears to be shared by all particles, irrespective of their quantum numbers. Antimatter phase is rational multiples of . ...in searching for new mass triplets.
Interesting. From the figure and other similar figtures one indeed sees how very near to is consistent with all measurements of neutrino oscillations if one allows mass scale to vary. In TGD model for CKM matrix in terms of topological mixing matrices U and D for U and type quarks (sphere, torus, and sphere with two handles characterizing the topology of partonic 2-surface associated with quark) the sum of mass squared for non-mixed quarks is integer if one uses p-adic mass squared scale as unit (and different for different quarks). This integer is not changed in mixing.
Integers: p-adics? Complex numbers: rational multiples of .? Surfaces and spheres? Emergence of new dimensions? The same problem as in the genetic code.
What is the aim of mixing? Make the possible solutions as big as possible? The same as mutations in genetics?
Complex numbers are essential to spinors, which are a generalization of the tensors used in relativity. Twistors too. Pythagoras' theorem is wellknown.
Oscillations between matter and antimatter?
How does this double broken symmetry take place? Each kaon particle consists of a combination of a quark and an antiquark. The weak force makes them switch identities time and time again: the quark becomes an antiquark while the antiquark becomes a quark, thus transforming the kaon into its antikaon. Matter is just an oscillation. A kaon soliton between bosonic and fermionic states, between quantum world and real world? Between dense states and virtual states? Between matter and force. Fascinating!
Perturbative connectivity to a hypothetical liquid of noninteracting fermions ... as the interaction is slowly turned on from zero to its full strength, the original fermions turn into weakly interacting fermionic quasiparticles, but without a drastic reorganization of the low-energy Hilbert space or a phase transition. ... both (superconductivity and the fractional Hall effect) connect these exotic quantum liquids to certain ordinary Fermi liquids residing in unphysical Hilbert spaces... “(non) Fermi liquid” and “quasiparticles” are often used synonymously (hypothetical) By increasing the fermion density away from the relativistic quantum critical point, a state emerges with all the features of the Fermi liquid.Density, pressure, space, time... gives quasiparticles?
Volovik (anti-GUT) (2008) in Emergent physics: Fermi-point scenario
That we survive in our Universe is not the result of the anthropic principle (the latter chooses universes that are fine-tuned for life but have an extremely low probability). On the contrary, this simply indicates that our Universe is also natural, and its vacuum is generic, though it belongs to a different universality class of vacua, the vacua with Fermi points. In such vacua, the masslessness of fermions is protected by topology (combined with symmetry). The mass is determined by the hierarchy of energy scales. Gravity emerges together with fermionic and bosonic matter; emergent fermionic matter consists of massless Weyl fermions; emergent bosonic matter consists of gauge fields.Anyons that is neither fermions nor bosons. "the existence of topological states of matter whose quasiparticle excitations are neither bosons nor fermions, but are particles known as Non-Abelian anyons, meaning that they obey non-Abelian braiding statistics. ...the only such topological states thought to have been found in nature are fractional quantum Hall states, most prominently the v = 5/2 state."
Anyons are the intermediate state of Life?
Massless fermionic matter (Weyl fermions) and dyons, quasiparticles and quasiholes? Mass determined by the hierarchial energy scales? And hidden gauge fields? How is E=mc^2 true then? It is about a closed Universe. Our Universe is open.
To be continued.
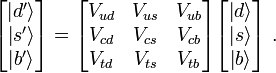
M. Sheppeard has published her paper about CKM mixing and MNS mixing (the leptonic variant) now.
SvaraRaderahttp://vixra.org/pdf/1008.0015v1.pdf
Quote:
SvaraRaderaThe new result, announced in June and submitted to the journal Physical Review Letters, appears to be one of the first observed violations of CP symmetry: the theory that matter and antimatter should behave in the same way. CP symmetry violation has been seen before in quarks, another type of elementary particle that makes up protons and neutrons, but never in neutrinos or electrons.
The finding could also force physicists to revise their Standard Model, which catalogs all of the known particles that make up matter. The model now posits only three flavors of neutrino, but a fourth (or fifth or sixth) may be necessary to explain the new results.
So far, the researchers have enough data to present their results with a confidence level of just below 99.7 percent (also called 3 sigma), which is not high enough to claim a new discovery.
Since the 1960s, physicists have been gathering evidence that neutrinos can switch, or oscillate, between three different flavors — muon, electron and tau, each of which has a different mass. However, they have not yet been able to rule out the possibility that more types of neutrino might exist.
In 1990, the LSND reported that a higher-than-expected number of antineutrinos appeared to be oscillating over relatively short distances, which suggests the existence of a fourth type of neutrino, known as a “sterile” neutrino.
http://web.mit.edu/newsoffice/2010/neutrinos-0812.html
The hints at a fourth generation has created much 'wind in the teacup'. Now the number may be growing?
There is an infinite hierarchy? Mass follows that hierarchy?